왕실의 기사 (구현 알고리즘)
왕실의 기사 (구현 알고리즘)
[문제1] 왕실의 기사#
[문제] 왕실의 기사 : 문제 설명#
행복 왕국의 왕실 정원은 체스판과 같은 8 × 8 좌표 평면이다. 왕실 정원의 특정한 한 칸에 나이트가 서있다. 나이트는 매우 충성스러운 신하로서 매일 무술을 연마한다 나이트는 말을 타고 있기 때문에 이동을 할 때는 L자 형태로만 이동할 수 있으며 정원 밖으로는 나갈 수 없다 나이트는 특정 위치에서 다음과 같은 2가지 경우로 이동할 수 있다
- 수평으로 두 칸 이동한 뒤에 수직으로 한 칸 이동하기
- 수직으로 두 칸 이동한 뒤에 수평으로 한 칸 이동하기
이처럼 8 × 8 좌표 평면상에서 나이트의 위치가 주어졌을 때 나이트가 이동할 수 있는 경우의 수를 출력하는 프로그램을 작성하라. 왕실의 정원에서 행 위치를 표현할 때는 1부터 8로 표현하며, 열 위치를 표현할 때는 a 부터 h로 표현한다
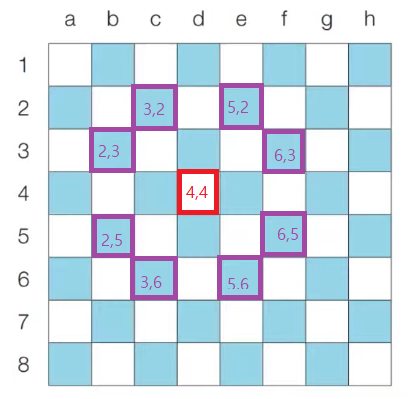
c2에 있을 때 이동할 수 있는 경우의 수는 6가지이다 a1에 있을 때 이동할 수 있는 경우의 수는 2가지이다 d4에 있을 때 이동할 수 있는 경우의 수는 8가지이다.
[문제] 조건#
조건 풀이시간 20분 시간제한 1초, 메모리 128mb
입력 첫째 줄에 8x8 좌표 평면상에서 현재 나이트가 위치한 곳의 좌표를 나타내는 두 문자로 구성된 문자열이 입력된다. 입력 문자는 a1 처럼 열과 행으로 이뤄진다.
출력 첫째 줄에 나이트가 이동할 수 있는 경우의 수를 출력하시오.
입력 예시 a1
출력 예시 2
아이디어#
- 모든 경우를 탐색하는 완전탐색 유형의 문제이다
- 문자 -> 아스키 코드를 반환 하는 ord(‘a’) 를 알아야 한다.
참고 <-> chr(97)
royal_knight.py#
n = str(input())
x = ord(n[0:1])
y = n[1:2]
#print(n[0:1])
#print(n[1:2])
#print(chr(104))
#print(ord('a'))
mv = [0 , 1, 2, 3, 4, 5, 6, 7]
dx = [-1, +1, +2, +2, +1, -1, -2, +2]
dy = [-2, -2, -1, +1, +2, +2, +1, -1]
count = 0
for move in mv :
if( ord('a') <= int(x)+dx[move] <= ord('h')
and 1 <= int(y)+dy[move] <= 8) :
count += 1
print(count)
royal_knight2.py#
input_data = input()
row = input_data[1]
column = int(ord(input_data[0]))- int(ord('a')) +1
steps = [(-2, -1), (-2, +1), (-1, +2), (+1,+2), (+2, +1), (+2, -1), (+1, -2), (-1, +2)]
count = 0
for step in steps :
if( 1 <= step[0]+int(row) <= 8 and 1 <= step[1]+int(column) <= 8 ) :
count += 1
print(count)
파이썬 모범답안#
input_data = input()
row = int(input_data[1])
column = int(ord(input_data[0]))- int(ord('a')) +1
steps = [(-2, -1), (-2, +1), (-1, +2), (+1,+2), (+2, +1), (+2, -1), (+1, -2), (-1, +2)]
result = 0
for step in steps :
next_row = step[0]+row
next_column = step[0]+column
if( 1 <= next_row <= 8 and 1 <= next_column <= 8 ) :
result += 1
print(result)
놓친 아이디어#
- input_data = input(), input_data[0],input_data[1] 로 접근 할 수 있는것을 더 복잡하게 잘라냈다.
- int(ord(input_data[0])) - int(ord(input_data[a])) + 1 을 사용하여 1 ~ 8로 더 간편히 조회가능.
- 이동 관련해서 dx,dy 각각 배열을 만들었지만, row, column을 하나의 데이터로 묶어서 사용할 수도 있다.
RoyalKnight.java#
package ex.algorithm.implement;
import java.util.ArrayList;
import java.util.Scanner;
public class RoyalKnight{
public static void main(String[] args) {
int result = 0;
Scanner sc = new Scanner(System.in);
String input_data = sc.nextLine();
int row = Integer.parseInt(input_data.substring(1,2));
int column = (int)input_data.substring(0,1).charAt(0) - (int) 'a' + 1;
ArrayList steps = new ArrayList<ArrayList<Integer[]>>();
steps.add(new Integer[]{-2,-1});
steps.add(new Integer[]{-2,+1});
steps.add(new Integer[]{-1,+2});
steps.add(new Integer[]{+1,+2});
steps.add(new Integer[]{+2,+1});
steps.add(new Integer[]{+2,-1});
steps.add(new Integer[]{+1,-2});
steps.add(new Integer[]{-1,-2});
for (Object obj : steps) {
Integer[] step = (Integer[])obj;
int next_row = row + step[0];
int next_column = column + step[1];
if((1 <= next_row && next_row <= 8) && (1 <= next_column && next_column <= 8)) {
result++;
}
}
System.out.println(result);
}
}
이 자료는 나동빈님의 이코테 저서를 보고 정리한 자료입니다.